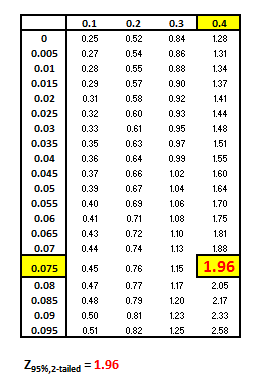
Z Table - Normal Distribution

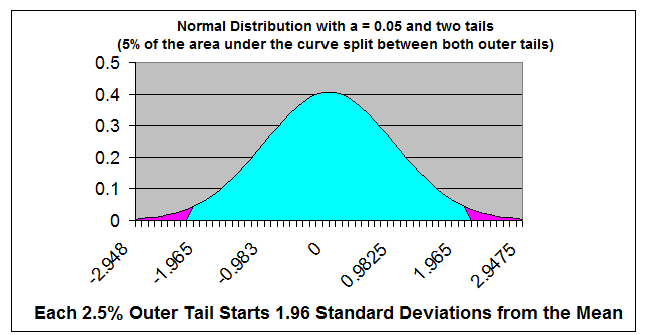
The two-tailed Z score tells how many standard deviations from the mean are required to contain a specified percentage of the area under the Normal Curve.

In the case of this two-tailed, 95% Z score, 95% of the total area under the Normal curve is contained within 1.96 standard deviations from the mean in either direction of the mean.

For this two-tailed test, the remaining 5% of the area under the Normal Curve is split between the 2 outer tails (hence the name - "two-tailed). Each outer tail holds 2.5% of the total area under the Normal Curve. This leave 47.5% of the total area between the outer tail and the mean on each side of the mean.

The Z score of 1.96 corresponds to this remaining 47.5% of the total area between the mean and each outer tail containing 2.5% of the total area.